Chapter 6 The Bootstrap
One can directly simulate from the distributions only when one is certain about the distribution of the population. Often in reality, one does not know the population characteristics and hence one has to resort to bootstrap methods. These methods do not make any assumptions on the population distribution and work with sample data alone.
6.1 Key Idea
The key idea of bootstrap is that it uses the given sample to create a new distribution, called the bootstrap distribution, that approximates the sampling distribution for the sample statistic
The original sample approximates the populaton from which it was drawn. So resamples from this sample approximate what we would get if we took many samples from the population. The bootstrap distribution of a statistic, based on many resamples, approximates the sampling distribution of the statistic, based on many samples.
(as_tibble(NCBirths2004)%>%summarize(mean(Weight)))
## # A tibble: 1 x 1
## `mean(Weight)`
## <dbl>
## 1 3448.
boot_samples <- replicate(10000, {
mean(sample(NCBirths2004$Weight, 1009, TRUE))
})
df <- data.frame(samples = boot_samples)
ggplot(df, aes(x=samples)) + geom_histogram()
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.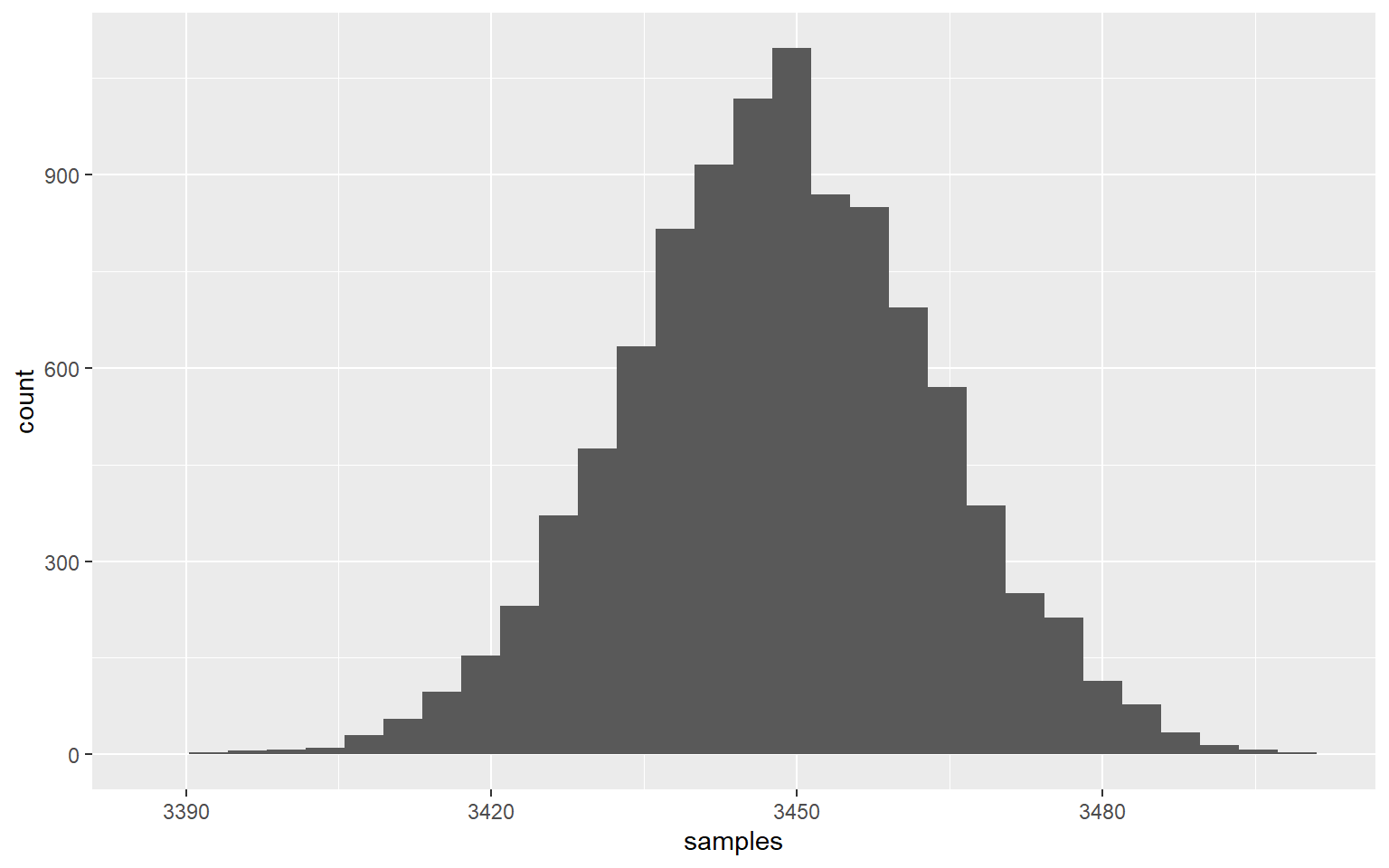
ggplot(df)+ geom_qq(aes(sample=samples))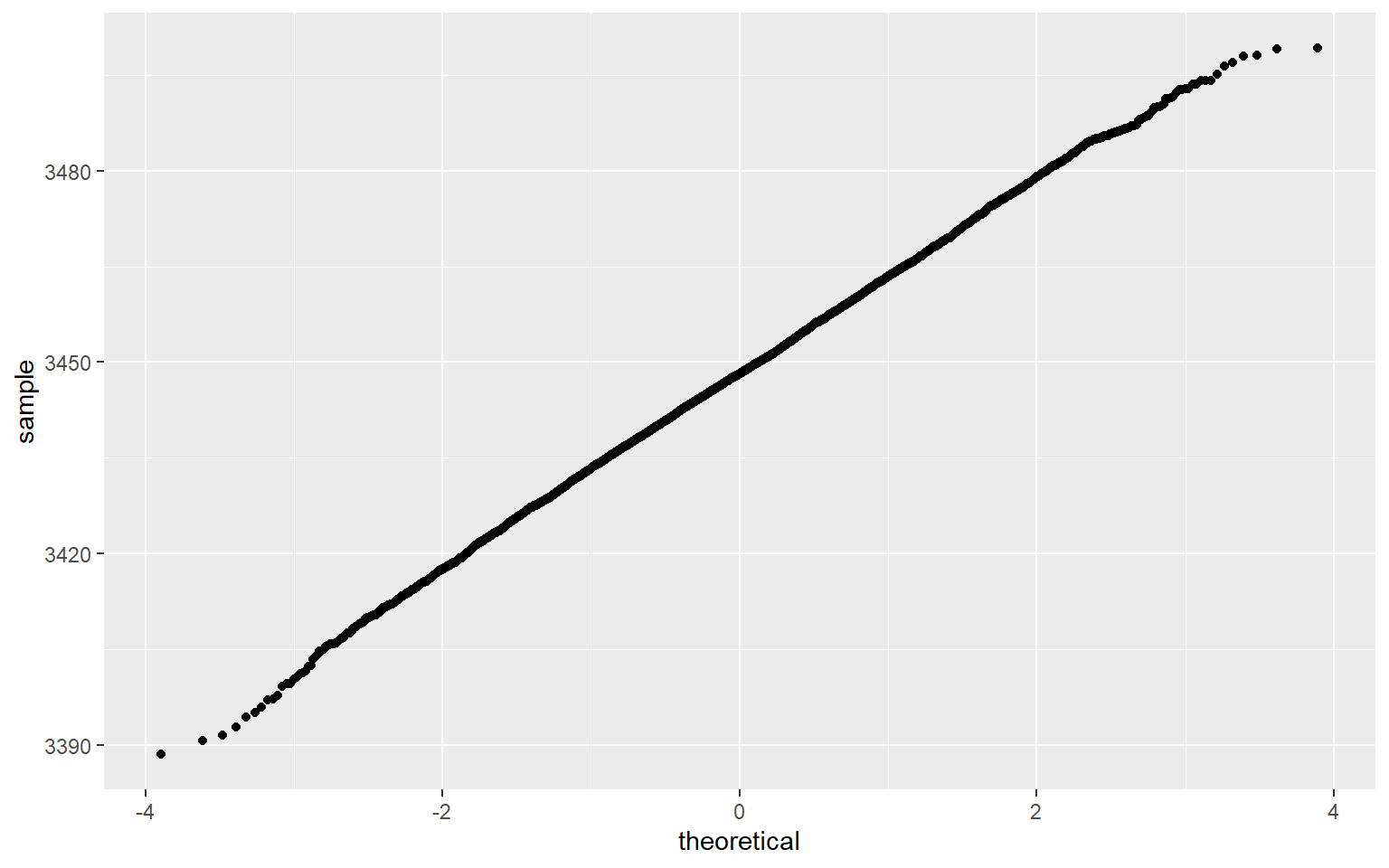
6.2 Bootstrap SE
The bootstrap standard error of a statistic is the standard deviation of the bootstrap distribution of that statistic
6.3 Plug-in Principle
The idea behind the bootstrap is the plug-in principle - that if something is unknown, we plug in an estimate for it
To estimate a parameter, a quantity that describes the population, use the statistic that is the corresponding quantity for the sample. We are using the sample as the estimate of the original data
6.4 Parametric Bootstrap
One might want to make some distributional assumption for the population and then estimate the parameters of the distribution based on the sample. For example, one can assume that the data comes from a gamma distribution and then estimate the parameters of the gamma distribution from the sample. One these parameters are estimated, one can then proceed to generate random samples from it. This is called Parametric Bootstrap
6.5 Estimators
The statistics that we bootstrap are generally called estimators, statistics that estimate a paramter.
6.6 Bootstrap percentile CI
The interval between the 2.5 and 97.5 percentiles of the bootstrap distribution of a statistic is a 95% bootstrap percentile confidence interval for the corresponding parameter
6.7 Bootstrap bias
The bootstrap estimate of bias is \[ Bias_{boot}[\hat {\theta^\ast}] = E[\hat {\theta^\ast}] - \hat \theta \]
6.8 Accuracy
There are two sources of variation in a Bootstrap distribution 1. The original sample is chosen at random from the population 2. Bootstram resamples are chosen at random rom the original sample
6.9 Takeaways
- bootstrap is not used to get better parameter estimates because the bootstrap distributions are centered around statistic \(\hat \theta\) rather than the unnown population values. The bootstrap sampling is useful for quantifying the behavior of the parameter estimate, such as its standard error, skewness and bias, or for calculating confidence intervals
- In a permutation test, we sample without replacement from the pooled data. The permutation distribution corresponds to the sampling in a way that is consistent with the null hypothesis that the population means are the same
- The permutation distribution is used for a single purpose - calculate a p-value to see how extreme an observed statistic is, if the null hypothesis is true. The bootstrap is used for estimating the standard error, trimmed means, correlation coefficients
- The bootstrap can be use dwith a wide variety of statistics. It allows one to compute confidence intervals for any kind of statistic, even for those for which there are no easy formulas
- The bootstrap method allows us to check for bias by seeing whether the bootstrap distribution of a staistic is centered at the statistic of the original random sample
- THE KEY IDEA BEHIND BOOTSTRAP - Sample is an estimate of the population
- Recommended bootstap resamples is 10,000
- For most statistics, almost all the variation in bootstrap distributions comes from randomly selecting the original sample from the population. Reducing this variation requires collecting a larger sample.